(تصاویر) نسبیت خاص به زبان ساده؛ داستانی از پیوندهای نامرئی جهان
تصور کنید سوار قطاری در حال حرکت هستید. اگر توپی را به سمت جلو پرتاب کنید، ناظرهای داخل و خارج از قطار، سرعتهای متفاوتی را برای توپ بهدست میآورند. این موضوع کاملاً بدیهی بهنظر میرسد؛ اما اگر به جای توپ، یک پرتو نور را به سمت جلو بتابانید، چه اتفاقی میافتد؟ آیا سرعت نور هم مانند توپ تحتتأثیر حرکت قطار قرار میگیرد؟ این پرسش ساده، آلبرت اینشتین، نابغهی فیزیک را به سوی کشفی شگفتانگیز سوق داد.
اینشتین با انجام آزمایشهای ذهنی و محاسبات پیچیده، به نتیجهای عجیب، اما دقیق دست یافت؛ سرعت نور در خلأ همیشه ثابت است و تحتتأثیر حرکت منبع نور یا ناظر قرار نمیگیرد. این نتیجه، بنیان نظریهای جدید را بنا نهاد که به نسبیت خاص معروف شد.
زمان و طول در نسبیت خاص، مفاهیمی نسبی هستند
نسبیت خاص به ما میگوید که مفاهیمی مانند زمان و فضا، نسبی هستند و به چارچوب مرجع ناظر بستگی دارند. بهعبارت دیگر، زمانی که برای یک ناظر ثابت میگذرد، برای ناظری که با سرعت زیاد حرکت میکند، کندتر میگذرد. همچنین، طول اجسام در جهت حرکتشان کوتاهتر میشود. این پدیدهها که ممکن است در نگاه اول عجیب به نظر برسند، با انجام آزمایشهای متعدد، تأیید و امروزه بهعنوان بخشی جداییناپذیر از فیزیک مدرن پذیرفته شدهاند.
نظریه نسبیت خاص
فیزیک نیوتنی یا فیزیک کلاسیک در ابعاد بسیار کوچک و در سرعتهای بسیار بالا شکست میخورد و نمیتواند بسیاری از پدیدههای فیزیکی را توضیح دهد. برای توضیح پدیدههای فیزیکی در ابعاد بسیار کوچک، فیزیک کوانتوم وارد میدان شد و انقلابی بزرگ در علم فیزیک ایجاد کرد.
در سرعتهای بالا چه کاری میتوانیم انجام دهیم؟ برای پاسخ به این پرسش باید کمی با حرکت نسبی آشنا شویم. گالیله مفهومی را بهنام چارچوب مرجع اینرسی یا چارچوب مرجع لخت معرفی کرد: این چارچوب ثابت است و اجسام مختلف نسبت به آن حرکت میکنند. طبق این مفهوم، اندازهگیری سرعت حرکت جسمی دلخواه به چارچوب مرجعی که انتخاب میکنیم، بستگی دارد.
برای درک بهتر ایدهی گالیله، یک مثال ساده میزنیم؛ فرض کنید داخل قطاری نشستهاید که با سرعت ثابتی حرکت میکند. اگر مسافری در قطار شروع به قدم زدن کند، حرکتش از دید شما آرام و معمولی بهنظر میرسد و سرعت حرکت او را برابر با سرعت حرکت قدمهایش میدانید؛ اما اگر ناظری بیرون از قطار، روی زمین، این صحنه را تماشا کند، حرکت فرد را اینطور میبیند: سرعت قدم زدنش بهعلاوهی سرعت حرکت قطار.
مدت زمانی را که ناظر داخل فضاپیما برای نور اندازه میگیرد، Δt0 مینامیم. اما این مدت زمان برای ناظرِ روی زمین، متفاوت است. زیرا فضاپیما نسبت به او حرکت میکند. از دیدِ ناظرِ روی زمین، مسیر حرکت نور، علاوهبر مؤلفهی عمودی، مؤلفهی افقی نیز خواهد داشت. در این حالت، ناظر زمینی، مسیر حرکت نور، داخل فضاپیما را بهصورت نشاندادهشده در تصویر زیر میبیند. این مسیر بسیار طولانیتر از مسیر عمودی نور (2D) است.
بهکمک قضیهی فیثاغورث میتوانیم s، وتر مثلث، را بهصورت زیر بهدست آوریم. از دید ناظر زمینی، مسافت طیشده توسط نور در فضاپیمای در حال حرکت، برابر 2s است. ازآنجاکه سرعت نور در تمام چارچوبهای مرجع لخت یکسان است، مدت زمانی که ناظرِ روی زمین برای نور اندازه میگیرد، برابر Δt و بزرگتر از Δt0 خواهد بود. به این پدیده، اتساع زمان (Time Dilation) میگوییم.
2s = c ∆t
همچنین، مقدار L، نصف مسافتِ طیشده توسط فضاپیما، بهصورت زیر بهدست میآید:
L = v (∆t)/2
v سرعتِ حرکت فضاپیما است. پس از انجام عملیات ریاضی و سادهسازی، زمانهای t∆ و Δt0 به شکل زیر به یکدیگر مربوط میشوند:
این آزمایش فکری نشان میدهد که زمان، مفهومی مطلق نیست و میتواند تحت شرایط مختلف، رفتار متفاوتی داشته باشد.
انقباض طول در نظریه نسبیت اینشتین
در بخشهای قبل در مورد دو فرضیهی نسبیت خاص و مفهوم اتساع زمان صحبت کردیم. نظریه نسبیت خاص، گامی بزرگ در علم فیزیک بود. شاید اتساع زمان عجیبترین مفهومی باشد که تابهحال شنیدهاید، اما این تنها آغاز ماجرا است. این نظریه نشان میدهد که نهتنها زمان، بلکه طول نیز نسبی است و بسته به سرعت شما، تغییر میکند.
وقتی سرعت شما به سرعت نور نزدیک شود، همهچیز تغییر میکند؛ نهفقط جریان زمان، حتی اندازهگیریهای شما از فضا نیز تغییر خواهند کرد. در این حالت، فاصلهها کوتاهتر بهنظر میرسند و این تغییرات دقیقاً مطابق پیشبینیهای ریاضی نظریه نسبیت خاص رخ میدهند.
نهتنها زمان، بلکه طول نیز نسبی است
این اتفاق به این دلیل رخ میدهد که اگر یک ناظر روی زمین و یک ناظر در یک فضاپیمایی سریع، زمان متفاوتی را برای یک رویداد ثبت کنند، پس باید فاصلههای متفاوتی هم برای آن رویداد بهدست آورند. چرا؟ چون هر دو ناظر بر سر سرعت نسبی میان خودشان توافق دارند.
هرچه سرعت حرکت بیشتر باشد، اجسام و فاصلهها کوچکتر بهنظر میرسند. به این پدیده، انقباض طول میگوییم. در تصویر زیر دو فضاپیما نشان داده شدهاند که با سرعت بسیار زیاد به سمت سیارهای دوردست، حرکت میکنند. در حالت یک، رویدادها را از دید ناظر روی زمین و در حالت دو، رویدادها را از دید ناظرِ داخل فضاپیما میبینیم.
فرمول انقباض طول در نظریه نسبیت خاص
تفاوت در اندازهگیری طول، بهخوبی توضیح میدهد که چرا دو ناظر، گذر زمان را متفاوت احساس میکنند. همچنین، این مسئله میتواند توضیح دهد که چرا ذراتِ سریعالسیر، خلاف انتظار ما رفتار میکنند.
بهعنوان مثال، ذرهای بهنام میون که نیمهعمرش در حالت سکون، تنها یک میلیونیم ثانیه است، در سرعتهای نزدیک به نور و بهدلیل اثرات نسبیتی، زمان برایش کندتر میگذرد و مسافتهای کوتاهتری را طی میکند. این موضوع باعث میشود میون بتواند بیشتر از آنچه انتظار میرود، زنده بماند و مسافت بیشتری را طی کند.
E=mc^2؛ همارزی جرم و انرژی در نسبیت خاص
اتساع زمان و انقباض طول، بدون شک شگفتانگیزترین نتایج نظریه نسبیت خاص اینشتین هستند، اما این پایان کار نیست. شاهکار دیگری نیز در این نظریه وجود دارد که با معادلهی E=mc^2، توصیف میشود؛ معادلهای که احتمالاً شناختهشدهترین فرمول در تاریخ علم است.
اگرچه افراد بسیاری این معادله را دیدهاند، تعداد کمی با مفهوم آن آشنا هستند. معادلهی E=mc^2 در مورد همارزی جرم (m) و انرژی (E) صحبت میکند. توضیح همارزی جرم و انرژی را با مفهومی بهنام تکانه (Momentum یا p) آغاز میکنیم. تمام اجسام تمایل به حفظ حالت فعلی خود دارند. بهعنوان مثال، اگر جسمی ساکن باشد، دوست دارد ساکن بماند یا اگر در حال حرکت باشد، دوست دارد به حرکتش ادامه دهد. با ترکیب اینرسی و حرکت، به مفهومی بهنام تکانه میرسیم.
همارزی جرم و انرژی یکی دیگر از نتایج شگفتانگیز نسبیت خاص است
به میزان حرکت یک جسم در حال حرکت، تکانه میگوییم. بهزبان ساده، تکانه، میزان تمایل جسمِ متحرک بهادامهی حرکت را نشان میدهد. هرچه جرم جسم بیشتر باشد (سنگینتر باشد) یا با سرعت بیشتری حرکت کند، تکانهی آن بزرگتر خواهد بود. در نتیجه، توقف یک کامیون در حال حرکت خیلی سختتر از یک دوچرخه در حال حرکت است، حتی اگر هر دو با سرعت یکسانی حرکت کنند.
همچنین، هرچه سرعت حرکت جسمی بزرگتر باشد، تکانهی آن نیز بزرگتر خواهد بود. با نزدیک شدن سرعت حرکت به سرعت نور، اثرات نسبیتی ظاهر میشوند. در این حالت، به تکانه باید بهصورت نسبیتی نگاه کنیم که بهصورت زیر بهدست میآید:
اگر فراتر از سرعت نور حرکت کنیم، یک اثر ممکن است قبل از علت خودش رخ دهد. این یعنی نقض علت و معلول. بههمین دلیل، باید بپذیریم که سرعت نور یک محدودیت فیزیکی و مرزی غیرقابل عبور است.
معادلهی E=mc^2 نتایج شگفتانگیزی دارد. طبق این معادله، جرم و انرژی همارز هستند و میتوانند به یکدیگر تبدیل شوند. جرم، نوعی انرژی است. برای آن که بفهمیم مقدار مشخصی از ماده، معادل چهمقدار انرژی است، باید جرم آن را در مجذور سرعت نور ضرب کنیم؛ عدد بهدستآمده بسیار بزرگ خواهد بود.
این کشف، درک ما را از جهان متحول کرد. انرژی، دیگر محدود به گرما، نور، حرکت یا الکتریسیته نیست؛ حالا میدانیم که ماده، یکی از بنیادیترین اشکال انرژی است.
مفهوم تصویری نسبیت خاص و نسبی بودن همزمانی
تا اینجا در مورد اتساع زمان، انقباض طول و همارزی جرم و انرژی صحبت کردیم. در این قسمت این نظریه را بهصورت تصویری و با مفهومی بهنام فضازمان، بررسی میکنیم.
اگر بخواهید دوستتان را در هر جایی از زمین ملاقات کنید، باید به او مختصات دقیق طول جغرافیایی، عرض جغرافیایی و ارتفاع آن مکان بدهید. اما برای ملاقات با دوستتان، علاوه بر مکان، باید زمان دقیقی را مشخص کنید.
جهان ما از چهار بُعد تشکیل شده است: سه بُعد فضایی (طول، عرض و ارتفاع) و یک بُعد زمانی. بهکمک این چهار بُعد میتوانید مکان و زمان دقیق هر رویدادی را مشخص کنید.
اما زمان را چگونه میتوانیم بهعنوان بُعد در نظر بگیریم؟ زمان برخلاف سه بُعد فضایی، برحسب متر یا اینچ اندازه گرفته نمیشود. بنابراین، اینگونه بهنظر میرسد که هیچ ارتباطی با سه بُعد فضایی ندارد. اما برخلاف تصور ما، زمان، همانند ابعاد فضایی، یکی از مؤلفههای بنیادی جهان است.
زمان و فضا بهقدری در هم تنیدهاند که آنها را نمیتوانیم جدا از یکدیگر تصور کنیم. بنابراین، فیزیکدانان به هندسهی جهان، نه بهعنوان فضا، بلکه بهعنوان فضازمان اشاره میکنند.
در اواخر قرن نوزدهم، مشکلی جدی در علم فیزیک بهوجود آمد. قوانین حرکت نیوتن و معادلات ماکسول درمورد الکتریسیته و مغناطیس، با هم سازگار نبودند. موضوع بحثبرانگیز سرعت نور بود. ماکسول نشان داد که نور نوعی موج است؛ برطبق معادلات ماکسول، سرعت این موج حدود ۳۰۰ هزار متربرثانیه پیشبینی شد.
سؤال مهمی که در آن زمان مطرح شد آن بود که فردِ متحرک، چه مقداری برای سرعت نور بهدست میآورد. برطبق قوانین نیوتن، سرعت حرکت فرد بر مقدار اندازهگیری شده برای سرعت نور تأثیر میگذارد؛ اما معادلات ماکسول نشان میدادند که نور با سرعت ثابتی حرکت میکند.
در سال ۱۸۸۷، دو دانشمند آمریکایی به نامهای مایکلسون و مورلی آزمایشی طراحی کردند که با دقت بالایی، سرعت نور را در جهت حرکت زمین اندازهگیری میکرد. انتظار میرفت عدد بهدستآمده برابر سرعت نور به علاوهی سرعت چرخش زمین باشد؛ اما نتیجهای که به دست آمد، جامعهی علمی را شوکه کرد: سرعت نور ثابت بود و به حرکت زمین وابسته نبود.
همانطور که گفتیم زمان و مکان، واحدهای اندازهگیری متفاوتی دارند. برای حل این مسئله، مینکوفسکی پیشنهاد داد زمان را بهعنوان طول بیان کنیم. این کار را با ضرب زمان در سرعت نور (ct) انجام میدهیم. در نتیجه، محور زمان را ct مینامیم.
فرض کنید در نمودار فضازمان دوبعدی، منبع نوری را روشن میکنیم. این رویداد را رویداد A مینامیم. نور در تمام جهتها منتشر میشود و با گذشت زمان، مرزهای گسترش نور را بهشکل یک مخروط، بهنام مخروط نور، میبینیم.
ممکن است در این مرحله از خود بپرسید، نظریه نسبیت چگونه وارد این معادله میشود؟ چگونه حرکت ناظران مختلف با سرعتها و در چارچوبهای مرجع متفاوت، میتواند بر مخروط نور تأثیر بگذارد.
برای پاسخ به این پرسشها، بار دیگر مخروط نوری را در نظر میگیریم و فرض میکنیم منبع نور، نسبت به ناظری که بدون حرکت ایستاده، ساکن است. اگر دو آشکارساز نور را در فاصلههای مساوی نسبت به منبع نور قرار دهیم، آشکارسازها بهطور همزمان، برخورد نور به خود را تشخیص میدهند. این موضوع تا زمانی درست است که آشکارسازها، منبع نور و ناظر حرکت نکنند. در این حالت، خطهای جهانی آشکارسازها و منبع نور عمود هستند.
تاکنون، رویدادها را از دید ناظر A که ساکن است، بررسی کردیم. اما از دید آشکارسازها و منبع نور، اتفاقات بهگونهی متفاوتی رخ میدهند. حال فرض کنید ناظرِ B همراه با آشکارسازها و منبع نور، با سرعت یکسانی حرکت میکند. از دید B، نور همزمان به دو آشکارساز میرسد.
ناظر B، خودش، آشکارسازها و منبع نور را ساکن میبیند و ناظرِ A را میبیند که به سمت چپ حرکت میکند. همچنین، از دید ناظر B، خطوط جهانی اجسام و مخروط نوری، کاملاً عمودی هستند.
- دیدگاه ناظر B:
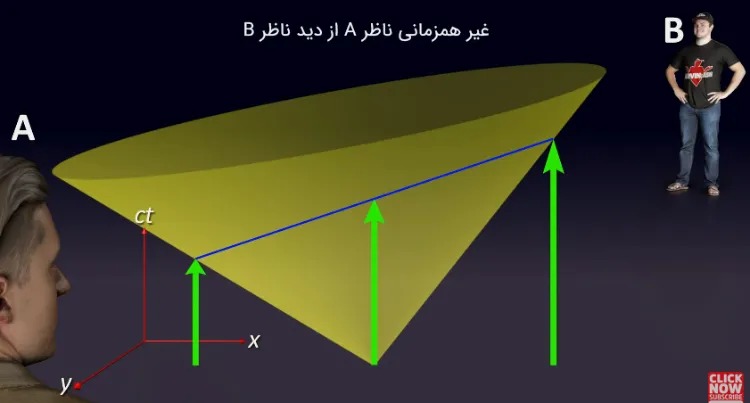
جمعبندی: نسبیت خاص و درهمتنیدگی فضا و زمان
نظریهی نسبیت خاص که توسط آلبرت اینشتین در سال ۱۹۰۵ ارائه شد، انقلاب بزرگی در درک ما از فضا، زمان و ماده ایجاد کرد. این نظریه نهتنها برداشت سنتی ما از فضا، زمان و ماده را به چالش کشید، بلکه تصویری تازه و عمیق از واقعیت ارائه کرد که تأثیرات آن تا به امروز در دنیای علم و تکنولوژی ادامه دارد.
یکی از مفاهیم کلیدی نسبیت خاص این است که زمان و فضا مطلق نیستند. برخلاف باورهای پیشین که زمان و فضا را مستقل از یکدیگر و ثابت میپنداشتند، اینشتین نشان داد که این دو به هم گره خوردهاند و مفهومی جدید به نام فضازمان را تشکیل میدهند. در این چارچوب، پدیدههایی که برای یک ناظر بهطور همزمان اتفاق میافتند، ممکن است برای ناظری دیگر در زمانهای مختلف رخ دهند. به عبارت دیگر، همزمانی مطلق معنایی ندارد و هر چیزی به چارچوب مرجع ناظر بستگی دارد.
یکی از شگفتانگیزترین پیامدهای این نظریه، ثابت بودن سرعت نور است. چه ساکن باشید و چه با سرعتی نزدیک به سرعت نور حرکت کنید، سرعت نور برای شما و همهی ناظران، بدون تغییر باقی میماند. این ویژگی خاص، زیربنای بسیاری از قوانین جدید فیزیک است و مفاهیمی چون انقباض طول و اتساع زمان را توضیح میدهد. برای مثال، از دید ناظری که در چارچوب مرجعی سریع حرکت میکند، زمان آهستهتر میگذرد و اجسام کوتاهتر به نظر میرسند.
نظریهی نسبیت خاص، نه فقط یک ایدهی فلسفی یا نظری، بلکه ابزاری عملی برای فهم جهان است. از مهمترین کاربردهای آن میتوان به سیستمهای موقعیتیابی جهانی (GPS) اشاره کرد. ماهوارههای GPS، به دلیل حرکت سریع و قرار داشتن در میدان گرانشی متفاوت، با اتساع زمان روبهرو هستند. بدون در نظر گرفتن اصلاحات ناشی از نسبیت خاص، دادههای GPS با خطای قابل توجهی مواجه میشدند و عملاً کارایی خود را از دست میدادند.
اما شاید جذابترین جنبهی نسبیت خاص، تغییری باشد که در نگاه ما به جهان ایجاد کرده است. این نظریه نشان میدهد که جهان مکانی ایستا و غیرقابل تغییر نیست، بلکه پویا و متغیر است. چنین بینشی ما را به سمت پرسشهای عمیقتری دربارهی ماهیت واقعیت و جایگاه ما در کیهان رهنمون میکند.
منبع: خبرآنلاین
منبع: faradeed-225517